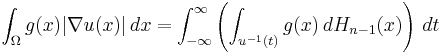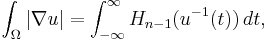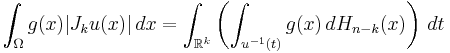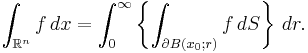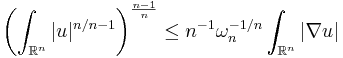Coarea formula
In the mathematical field of geometric measure theory, the coarea formula expresses the integral of a function over an open set in Euclidean space in terms of the integral of the level sets of another function. A special case is Fubini's theorem, which says under suitable hypotheses that the integral of a function over the region enclosed by a rectangular box can be written as the iterated integral over the level sets of the coordinate functions. Another special case is integration in spherical coordinates, in which the integral of a function on Rn is related to the integral of the function over spherical shells: level sets of the radial function. The formula plays a decisive role in the modern study of isoperimetric problems.
For smooth functions the formula is a result in multivariate calculus which follows from a simple change of variables. More general forms of the formula for Lipschitz functions were first established by Herbert Federer (Federer 1959), and for Sobolev functions by Fleming & Rishel (1960).
A precise statement of the formula is as follows. Suppose that Ω is an open set in Rn, and u is a real-valued Lipschitz function on Ω. Then, for an L1 function g,
where Hn − 1 is the (n − 1)-dimensional Hausdorff measure. In particular, by taking g to be one, this implies
and conversely the latter equality implies the former by standard techniques in Lebesgue integration.
More generally, the coarea formula can be applied to Lipschitz functions u defined in Ω ⊂ Rn, taking on values in Rk where k < n. In this case, the following identity holds
where Jku is the k-dimensional Jacobian of u.
Applications
- Taking u(x) = |x − x0| gives the formula for integration in spherical coordinates of an integrable function ƒ:
- Combining the coarea formula with the isoperimetric inequality gives a proof of the Sobolev inequality for W1,1 with best constant:
-
- where ω −1/n is the volume of the unit ball in Rn.
See also
References
- Federer, Herbert (1969), Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, Band 153, New York: Springer-Verlag New York Inc., pp. xiv+676, ISBN 978-3540606567, MR0257325.
- Federer, H (1959), "Curvature measures", Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 93, No. 3) 93 (3): 418–491, doi:10.2307/1993504, JSTOR 1993504.
- Fleming, WH; Rishel, R (1960), "An integral formula for the total gradient variation" (PDF), Archiv der Mathematik 11 (1): 218–222, doi:10.1007/BF01236935, http://www.springerlink.com/index/WV67N13464926501.pdf
- Malý, J; Swanson, D; Ziemer, W (2002), "The co-area formula for Sobolev mappings" (PDF), Transactions of the American Mathematical Society 355 (2): 477–492, doi:10.1090/S0002-9947-02-03091-X, http://www.ams.org/tran/2003-355-02/S0002-9947-02-03091-X/S0002-9947-02-03091-X.pdf.